Estimaciones de Primas por Plazo
(Ir directamente a las estimaciones)
|
La tasa de largo plazo asociada a bonos nominales se puede descomponer de diferentes maneras y con diferentes propósitos. Un caso conocido es la descomposición en la tasa real, la inflación esperada y la prima por riesgo inflacionario, lo que se podría considerar como una generalización a la célebre ecuación de Fisher. Otra descomposición consiste en expresar a la estructura temporal de tasas de interés en función de una suma ponderada de vectores (ortogonales entre sí). Esta estructura naturalmente incluye a la tasa de interés de largo plazo, lo que se logra a través de la metodología de componentes principales. Una descomposición que ha retomado importancia en los últimos años es con la cual se obtiene la llamada prima por plazo. Esta consiste en dos componentes: el promedio esperado de tasas de interés de corto plazo y, precisamente, la prima por plazo. Esta descomposición ha cobrado importancia en el contexto de la política monetaria. Ello se debe, en buena medida, a que se tiene un gran interés en entender cómo las políticas monetarias no convencionales han afectado a los diferentes componentes de las tasas de interés. Una posible interpretación del promedio esperado de tasas de interés de corto plazo es la tasa de interés de largo plazo que prevalecería si el agente fuese neutral al riesgo. La intuición es directa. Para un agente que sea neutral al riesgo todas sus primas por riesgo deben de ser igual a cero. Así, si uno estima la tasa de interés de largo plazo neutral al riesgo, al estandarizarla por la tasa de interés, se obtiene la prima por plazo. En otras palabras, la estimación de la tasa de interés de largo plazo neutral al riesgo permite la identificación de la prima por plazo. Convencionalmente, se explica a la prima por plazo como la compensación al tenedor de un bono de largo plazo por haber invertido en el mismo en lugar de haber invertido en los bonos de corto plazo de manera consecutiva. Sin embargo, una interpretación más general, es que la prima por plazo captura los riesgos por los cuales el tenedor de un bono nominal de largo plazo es compensado, notablemente los riesgos por liquidez e inflación. Para ser específicos, como es el caso de todos los instrumentos financieros, no todos los riesgos son compensados, por ejemplo, los riesgos idiosincráticos a un instrumento no son compensados. Es conveniente hacer notar que algunas políticas no convencionales pueden afectar diferentes elementos de la descomposición. Por ejemplo, los anuncios de guía prospectiva (forward guidance) de alguna autoridad monetaria sobre mantener la tasa de interés de corto plazo en un nivel por un periodo de tiempo determinado debiesen, en principio, afectar el promedio esperado de tasas de interés de corto plazo. De manera similar, otras políticas pudiesen afectar a la prima por plazo en la medida en que estas impacten los riesgos a los cuales el tenedor de bonos de largo plazo es compensado. La estimación de la prima por plazo requiere de un modelo econométrico. En este caso, se optó por la metodología y el modelo propuestos por Adrian, Crump y Moench (2013, ACM). Lo anterior se debe por las siguientes razones: Dicho lo anterior, es conveniente subrayar las siguientes salvedades. La estimación de la prima por plazo depende tanto del modelo utilizado como de las variables económicas utilizadas como insumos. En este caso se utiliza un modelo afín de tasas de interés y como insumos a las tasas de interés a diferentes plazo. La estimación también depende de la muestra utilizada. Lo anterior se deriva del hecho de que las tasas de interés son, por lo general, procesos estocásticos persistentes. El nivel de la prima por plazo es uno de los estadísticos que resulta ser más sensible a la elección del modelo, los insumos y la muestra utilizados. La consideración de estas salvedades es especialmente relevante cuando se comparan diferentes estimaciones de la prima por plazo, incluso las aquí mostradas. Sin embargo, la dinámica de la prima por plazo es más robusta a las referidas variantes. Analíticamente, se tiene la siguiente expresión: |
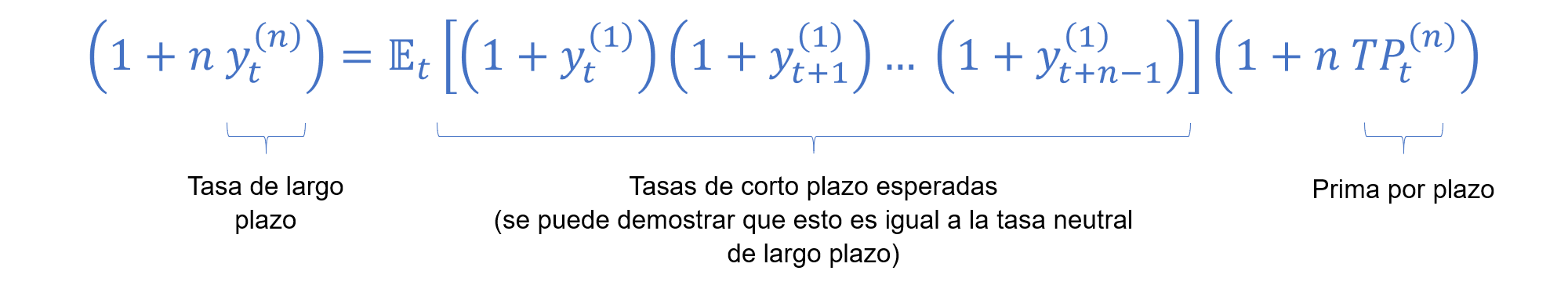
|
|
|
Referencias de estas estimaciones:
LATAM:Otras Referencias Útiles:
Seleccione los paises para mostrar las estimaciones de sus primas por plazo
|
|
|
|
|
- Los fechas de inicio de los datos son: Brasil (27-mar-2007), Chile (29-sep-2005), Colombia (28-abr-2006), México (2-ene-2004) y Perú (28-abr-2006). Estas fechas dependen de la disponibilidad de datos para cada economía.
- Para nuestra estimación de la prima por plazo para las economías latinoamericanas (LATAM) usamos promedios ponderados por PIB PPP en dólares internacionales de nuestras primas por plazo individuales. LATAM: Brasil, Colombia, Chile, México y Perú. Este promedio solo considera el periodo para el cual los datos están disponibles para todas las economías. De otra manera pudiera haber variaciones en los promedios de las primas por plazo debido a la inclusión de nuevas series.
- El modelo para las primas por plazo se reestima una vez al mes. Esto puede resultar en cambios menores en las estimaciones históricas de la descomposición de las tasas de los bonos.
- Fuentes: Estimaciones propias con insumos de Bloomberg, Valmer y WEO, Abril 2020 para: Brasil, Colombia, Chile, México y Perú. Adrian et al. (2013) para los EE.UU.
Para obtener las estimaciones diarias, por favor consulte las instrucciones .

